How does the `predict` method in an SVM implementation determine the classification of a new data point?

/ / Published in Artificial Intelligence, EITC/AI/MLP Machine Learning with Python, Support vector machine, Completing SVM from scratch, Examination review

The `predict` method in a Support Vector Machine (SVM) is a fundamental component that allows the model to classify new data points after it has been trained. Understanding how this method works requires a detailed examination of the SVM's underlying principles, the mathematical formulation, and the implementation details.

Basic Principle of SVM

Support Vector Machines are supervised learning models that are used for classification and regression tasks. The primary objective of an SVM is to find the optimal hyperplane that separates the data points of different classes with the maximum margin. This hyperplane is defined in a high-dimensional space, and the SVM model aims to maximize the distance between the closest points of the classes, known as support vectors, and the hyperplane.

Mathematical Formulation

The SVM model can be represented mathematically as follows:

1. Hyperplane Equation:

    \[ f(x) = w \cdot x + b \]

where w is the weight vector, x is the input feature vector, and b is the bias term.

2. Decision Function:
The decision function for classification is given by:

    \[ \text{sign}(f(x)) = \text{sign}(w \cdot x + b) \]

This function determines the class of the input data point x. If the result is positive, the data point is classified into one class (e.g., +1), and if negative, it is classified into the other class (e.g., -1).

Training the SVM

During the training phase, the SVM algorithm solves a convex optimization problem to find the optimal values of w and b. The objective is to minimize the following cost function:

    \[ \frac{1}{2} ||w||^2 + C \sum_{i=1}^{n} \xi_i \]

subject to the constraints:

    \[ y_i (w \cdot x_i + b) \geq 1 - \xi_i \quad \text{and} \quad \xi_i \geq 0 \]

where \xi_i are slack variables that allow for some misclassification in the case of non-linearly separable data, and C is a regularization parameter that controls the trade-off between maximizing the margin and minimizing the classification error.

Kernel Trick

For non-linearly separable data, SVMs use the kernel trick to map the input features into a higher-dimensional space where a linear hyperplane can separate the data. Common kernels include the polynomial kernel, radial basis function (RBF) kernel, and sigmoid kernel. The kernel function K(x_i, x_j) computes the inner product in the transformed feature space without explicitly performing the transformation.

The `predict` Method

Once the SVM model is trained, the `predict` method is used to classify new data points. The steps involved in the `predict` method are as follows:

1. Compute the Decision Function:
For a new data point x, the decision function is computed as:

    \[ f(x) = \sum_{i=1}^{n} \alpha_i y_i K(x_i, x) + b \]

where \alpha_i are the Lagrange multipliers obtained during training, y_i are the labels of the training data points, x_i are the support vectors, and K(x_i, x) is the kernel function.

2. Determine the Class Label:
The class label of the new data point is determined by the sign of the decision function:

    \[ \text{predict}(x) = \text{sign}(f(x)) \]

If f(x) \geq 0, the data point is classified into the positive class (e.g., +1), and if f(x) < 0, it is classified into the negative class (e.g., -1).

Example Implementation

Below is a simplified example of how the `predict` method might be implemented in a basic SVM from scratch using Python:

{{EJS1}}
Detailed Explanation of the Example
1. Initialization:
 The `SVM` class is initialized with a specified kernel (default is 'linear') and a regularization parameter 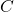C.
2. Training (`fit` method):
 The `fit` method is a placeholder for the actual training code, which would involve solving the optimization problem to find the Lagrange multipliers \alpha, support vectors, and the bias term b.
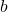3. Kernel Function:
 The `linear_kernel` method computes the inner product of two vectors, which is the simplest form of a kernel function. For more complex kernels, additional methods would be implemented.
4. Prediction (`predict` method):
 The `predict` method first selects the appropriate kernel function based on the specified kernel type. It then iterates over each new data point x and computes the decision function using the support vectors, their corresponding Lagrange multipliers, and labels. The sign of the decision function determines the class label of the new data point.
Practical Considerations
- Support Vectors:
 Only the support vectors contribute to the decision function. These are the data points that lie closest to the hyperplane and are critical in defining the margin.
- Regularization Parameter 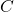C:
 The parameter 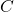C controls the trade-off between achieving a low error on the training data and maximizing the margin. A smaller 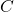C value allows for a larger margin with more misclassifications, while a larger 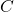C value aims for fewer misclassifications but a smaller margin.
- Kernel Choice:
 The choice of kernel function significantly impacts the SVM's performance. Linear kernels are suitable for linearly separable data, while non-linear kernels like RBF are used for more complex data distributions.
- Scalability:
 SVMs can be computationally intensive, especially for large datasets. The training complexity is typically 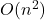O(n^2) to O(n^3), where n is the number of training samples. Techniques like the Sequential Minimal Optimization (SMO) algorithm are used to improve efficiency.The `predict` method in an SVM implementation is a critical component that leverages the trained model to classify new data points. By computing the decision function based on the support vectors, their corresponding Lagrange multipliers, and the kernel function, the method determines the class label of each new data point. Understanding the mathematical formulation and implementation details of the `predict` method provides valuable insights into the inner workings of SVMs and their application in machine learning tasks.
Other recent questions and answers regarding Completing SVM from scratch:
More questions and answers:
Tagged under: , , , , ,